العلاقات بين الزوايا في الرياضيات
تُعتبر الزوايا من المفاهيم الأساسية في الرياضيات، وهي تتعلق بالتداخل والتلاقي بين الخطوط والأشكال، وتُدرس العلاقات بين الزوايا عادةً لفهم الأنماط والترابطات التي تحدث بينها، علمًا بأن هذا يساهم في حل المشكلات الهندسية وتطبيقاتها في الحياة العملية، وفيما يأتي توضيح لأبرز العلاقات بين الزوايا في الرياضيات:
الزوايا المتكاملة
تعرف الزوايا المتكاملة (بالإنجليزية: Supplementary angles) في الرياضيات، بأنهما الزاويتان اللتان يكون مجموع قياسهما يساوي 180 درجة، أي أنه عند جمع الزاويتين المتكاملتين نحصل على زاوية مستقيمة، وبعبارة أخرى، يمكن التعبير عن الزوايا المتكاملة كالآتي:[١]
إذا كانت الزاوية A + الزاوية B = مئة وثمانين درجة (180 درجة)
فإن الزوايا A والزاوية B هما زوايا متكاملة
على سبيل المثال، الزاوية 60° + الزاوية 120° = 180°
إذًا الزوايا 60° و120° هما زوايا متكاملة.
الزوايا المتتامة
تعرف الزوايا المتتامة أو الزوايا التكميلية أو الزوايا المكملة (بالإنجليزية: Complementary Angles) في الرياضيات، بأنهما الزاويتان اللتان يكون مجموع قياسهما يساوي 90 درجة، أي أنه عند جمع الزاويتين المتتامتين أو المكملتين نحصل على زاوية قائمة، وبعبارة أخرى، يمكن التعبير عن الزوايا المتتامة أو المكملة كالآتي:[٢]
إذا كانت الزاوية C + الزاوية D = تسعين درجة (90 درجة)
فإن الزاويتين C و D هما زوايا متتامة أو مكملة.
على سبيل المثال، الزاوية 60° + الزاوية 30° = 90°
إذًا الزوايا 60° و30° هما زوايا متتامة أو مكملة.
الزوايا المتقابلة بالرأس
تعرف الزوايا المتقابلة بالرأس (بالإنجليزية: Vertically Opposite Angles) بأنها الزوايا التي تنشأ عن عند تقاطع خطين مع بعضهما البعض، حيث تسمى الزوايا المتقابلة المتبادلة، وتكون الزوايا المتقابلة بالرأس متساوية في القياس، ويمكن القول بتعبير آخر أن الزوايا التي تشترك في نفس الرأس أو نقطة الزاوية تكون متساوية، ويمكن التعبير عن الزوايا المتقابلة بالرأس كالآتي:[٣]
إذا كانت الزاوية E تقابل الزاوية F في الرأس
فإن الزاوية E = الزاوية F
الزوايا المتناظرة
تعرف الزوايا المتناظرة (بالإنجليزية: Corresponding Angles) بأنها الزوايا التي تنشأ عند تقاطع خطين مع خط ثالث، حيث تسمى الزوايا التي تقع في نفس الموضع النسبي زوايا متناظرة، وتكون الزوايا المتناظرة متساوية في القياس عندما يكون الخطان اللذين يتقاطعان مع الخط الثالث متوازيين، ويمكن توضيح الزوايا المتناظرة من خلال الصورة الآتية:[٤]

في الصورة السابقة:
∠p and ∠w
∠q and ∠x
∠r and ∠y
∠s and ∠z
الزوايا الداخلية المتبادلة
تعرف الزوايا الداخلية المتبادلة أو الزوايا المتبادلة داخليًا (بالإنجليزية: Alternate Interior Angles) بأنها الزوايا التي تنشأ عندما يتقاطع خطان مع خط ثالث، حيث تسمى الزوايا بين الخطين، وعلى جانبي الخط الثالث بالزوايا الداخلية المتبادلة، وتكون الزوايا الداخلية المتبادلة متساوية عندما يكون الخطان اللذان يتقاطعان مع الخط الثالث متوازيين، ويمكن توضيح الزوايا الداخلية المتبادلة من خلال الصورة الآتية:[٥]
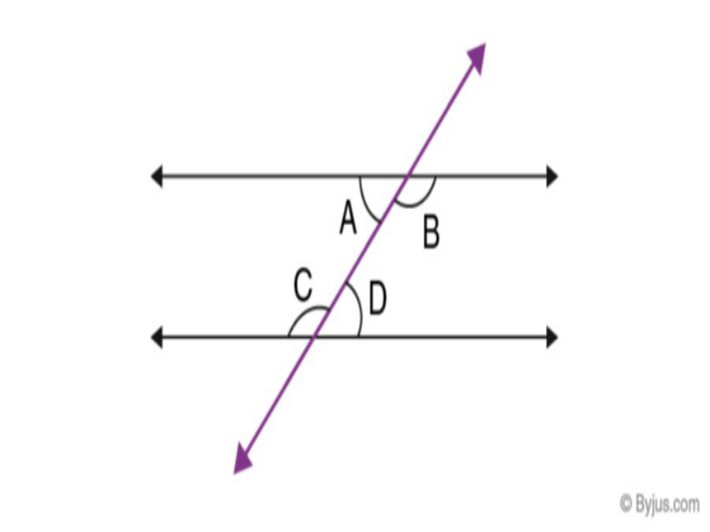
في الصورة السابقة:
∠A = ∠D
∠B = ∠C
الزوايا الخارجية المتبادلة
الزوايا الخارجية المتبادلة أو الزوايا المتبادلة خارجيًا (بالإنجليزية: Alternate Exterior Angles) بأنها الزوايا التي تنشأ عندما يتقاطع خطان مع خط ثالث، حيث تسمى الزوايا خارج الخطين، وعلى جانبي الخط الثالث بالزوايا الخارجية المتبادلة، وتكون الزوايا الخارجية المتبادلة متساوية عندما يكون الخطان اللذان يتقاطعان مع الخط الثالث متوازيين، ويمكن توضيح الزوايا الخارجية المتبادلة من خلال الصورة الآتية:[٦]
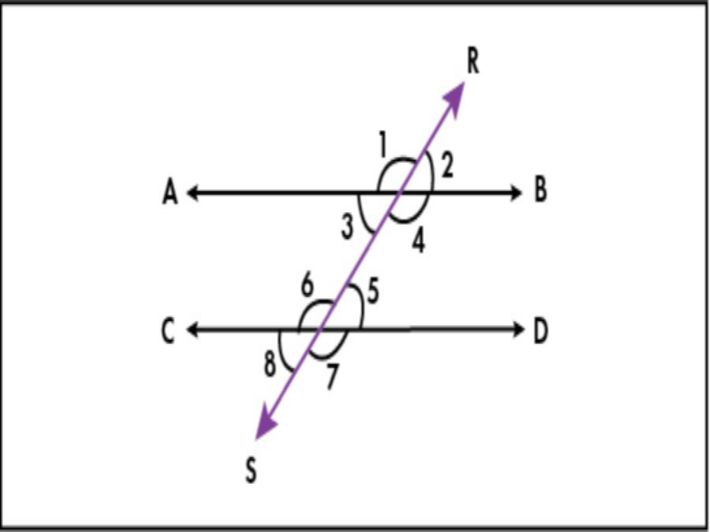
في الصورة السابقة:
∠3 = ∠ 5
∠4 = ∠6
∠2 = ∠8
∠1 = ∠7
المراجع
- ↑ "Supplementary Angles", mathsisfun, Retrieved 18/7/2023. Edited.
- ↑ "Supplementary And Complementary Angles", byjus, Retrieved 18/7/2023. Edited.
- ↑ "Vertically Opposite Angles", mathsisfun, Retrieved 18/7/2023. Edited.
- ↑ "Corresponding Angles", byjus, Retrieved 18/7/2023. Edited.
- ↑ "Alternate Interior Angles", byjus, Retrieved 18/7/2023. Edited.
- ↑ "Alternate Exterior Angles", byjus, Retrieved 18/7/2023. Edited.











